Contribute


How to contribute

Building materials in Brighton and Hove

Photo:Clay wall tiles

Clay wall tiles

All photographs by Ron Martin

Photo:Mathematical tiles

Mathematical tiles

Photo:Mathematical tiles

Mathematical tiles

Photo:Red tiles in header board

Red tiles in header board

Photo:Black glazed mathematical tiles

Black glazed mathematical tiles

Photo:Painted mathematical tiles

Painted mathematical tiles

Photo:Mathematical tiles

Mathematical tiles

Mathematical tiles
By Ron Martin

1. The two reasons for tiling walls
There are two reasons for covering the face of a building with tiles of some sort: one is to weatherproof it and the other is to alter the appearance of it. The principle form of vertical wall-tiling is plane tiles which are exactly the same tiles as I use on the roof but hung vertically, fixed normally to a timber-framed building. A very interesting form of material came into use during the 18th century and that is what is commonly known as mathematical tiles.

2. Mathematical tiles are common
A very interesting form of material came into use during the 18th century and that is what is commonly known as mathematical tiles. Their use in Sussex became very, very common in the closing years of the 18th century and the first twenty or so years of the 19th century.

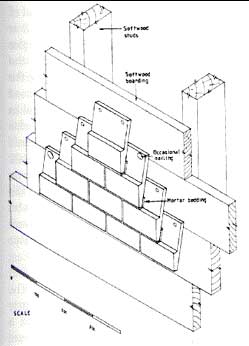
3. They are the same shape as brick
A mathematical tile is a clay tile which is the same shape as a brick. This was partly the reason they were used because in the 18th century to bring your house up to date you needed to have a brick face. To rebuild the front wall would have been expensive so the alternative was to cover the whole of the front face with mathematical tiles.

4. Mathematical tiles on bay windows
Towards the late 18th centuary a lot of mathematical tiles were used in Brighton on projecting bay windows where the bay was not carried down to the ground and therefore the bay was supported on the floor joists and therefore you wanted the material covering the bay window to be light so you would have used mathematical tiles in that form.

5. They come in all sorts of colours
Mathematical tiles came in all sorts of different colours, colours that bricks would have come in - reds and greys and whites. They also produced mathematical tiles with a black-glazed surface.

Image and text from the 1994 My Brighton museum exhibit
This page was added on 22/03/2006.

Comments:

I found this article extremely interesting having looked at a house in Hastings with them. But why were they called mathematical tiles?
By Barbara Young (20/08/2004)
As for why they're called 'mathematical' I have heard that nobody knows why. Also, there's another reason mathematical tiles were used: they were cheaper because they weren't subject to the Brick Tax (which existed between 1784 and 1850).
By Ian Gray (12/09/2004)
Mathematical tiles were subject to tax - the only exception was land drainage tiles.
By Jeremy Greenwood (07/03/2005)
You state projecting bay windows were carried on the floor joists. This is not always correct as the floor joists traditionally went across the building. Following a recent problem we believe the curved planks behind the tiles formed the structure.
By David Godfrey (08/06/2005)
Does anyone have a supplier for replacement tiles?
By John Moat (04/08/2005)
I was told that geometrical tiles are rare but can be found in Lewes. Is this the same as mathematical tiles? If they're different, what are they, where are they found; on what kinds of building and of what date and why were they introduced? I look forward to hearing from you.
By Jane Soole (24/08/2005)
This is a fascinating page which I looked up after being in Lewes at the weekend and being told to look out for 'geometrical tiles'. Are these the same as mathematical tiles? I see on another website that geometrical tiles refer to floor tiles.
By Jane Soole (25/08/2005)
I have some studies on mathematical tiles and can assist on sourcing new ones (refer you to possible makers). I have been in the brick industry for 20+ years and find this subject of great interest, if of little or no commercial value. Delighted to help researchers or repair problems.
By Duncan Cunningham (09/09/2005)
You say in 3. that 'tile is same shape as a brick' - but it clearly isn't. Very misleading - and you don't clarify what you mean with a photo or diagram.
By Tim - Lewes resident (09/03/2006)

We have a 1930s house with 2 bay windows. The top one has tiles underneath the window but we are having a problem with damp underneath the window in our bedroom. We think it is not insulated so when the the cold air is hitting the warm air it causing a damp problem. Has anyone had this problem and if so how can it be solved?

By Sarah Lambert (21/06/2007)

Sarah, your problem is most likley condensation caused by the warm air condensing when it hits the back of the cold tiles. You need a vapour barrier and to slow the temperature gradient using insulation. Using just insulation won't help as the moisture will still condense, but inside the insulation. The vapour barrier (polythene will do) needs to be on the warm side of the insulation. You will have to strip the plasterboard off on the inside to do this or take the tiles off and do it from outside. OR it could be just rain off the window sill blowing over the top of the top tiles.

By Guy Laughton (24/06/2007)

Is anyone aware of manufacturers of blue or black glazed mathematical tiles for a new build project? Many thanks.

By Julia Wedel (15/08/2007)

try Robus
http://www.robusceramics.co.uk/mathematicaltiles.html

By Julian Williams (24/01/2008)

I found this an interesting page and am glad to confirm that only land drains were exempt from brick tax. All bricks and tiles were subject to the tax which was introduced in 1784, with the exemption of land drainage. The tax was apparently removed from tiles in 1833 but stayed on bricks until about 1850. Interestingly I have found both, bricks and ridge tiles stamped with the word drain. One can only assume that the brick yards were on the fiddle!

By Karl Terry (05/03/2008)

I just wanted to say thanks for info on this page. As a Surveyor based in Newbury, Berkshire, I have been looking for a supplier of Mathematical Tiles for repairs on a listed building. This detail is very rare locally. In over 20 years practice this is only the second building with these tiles I have seen (and the first had them stripped about 10 years ago).

By Colin Gillah (06/11/2008)

Add a comment





Protected by FormShield